アンケートの作成方法(作り方のコツ)
アンケートは何人集めれば良いのか
 アンナさんに、アンケートの精度の話を聞きました。一般的な調査では何名ぐらい回答者を集めればいいのですか?
アンナさんに、アンケートの精度の話を聞きました。一般的な調査では何名ぐらい回答者を集めればいいのですか?
 アンナさんに、アンケートの精度の話を聞きました。一般的な調査では何名ぐらい回答者を集めればいいのですか?
アンナさんに、アンケートの精度の話を聞きました。一般的な調査では何名ぐらい回答者を集めればいいのですか?
 簡単な調査なら、200人ぐらいで間に合うことが多いのう。場合によっては、100人でも十分な場合もあるわい。少し細かい分析をするなら500人ぐらいかのう。
簡単な調査なら、200人ぐらいで間に合うことが多いのう。場合によっては、100人でも十分な場合もあるわい。少し細かい分析をするなら500人ぐらいかのう。
 ええっ!そんなに少なくていいのですか?1000人ぐらい必要なんじゃないですか?
ええっ!そんなに少なくていいのですか?1000人ぐらい必要なんじゃないですか? もちろん1000人ぐらい必要なケースもあるが、必要な回答人数はどれぐらいの精度を求めるかによるんじゃよ。
もちろん1000人ぐらい必要なケースもあるが、必要な回答人数はどれぐらいの精度を求めるかによるんじゃよ。 精度って、アンケート結果がどれだけ正しいかということですよね。
精度って、アンケート結果がどれだけ正しいかということですよね。 簡単にいうとそうじゃの。例えば商品パッケージを決めるためデザイン候補AとBのアンケートを実施する場合、回答者は5人でいいと思うかい?
簡単にいうとそうじゃの。例えば商品パッケージを決めるためデザイン候補AとBのアンケートを実施する場合、回答者は5人でいいと思うかい?
 それは、少ないような気がします。
それは、少ないような気がします。 じゃあ、100万人の回答者は必要かね?
じゃあ、100万人の回答者は必要かね? 確かに精度は上がりそうですが、それはそれで多すぎて大変そうな気がします。
確かに精度は上がりそうですが、それはそれで多すぎて大変そうな気がします。 そうじゃの。アンケートの回答者、つまりサンプル数は基本的に多ければ多いほど精度は高くなる。だからといって、上限なく回答者を集めるのもコスト的、労力的に大変じゃ。そこでアンケート実施時には、回答者の人数によって変わってくる誤差率を考慮する必要がある。誤差率というのは、文字通りアンケート結果にどの程度の誤差があるかをあらわすもので、精度とは表裏一体の関係にあるものじゃ。
そうじゃの。アンケートの回答者、つまりサンプル数は基本的に多ければ多いほど精度は高くなる。だからといって、上限なく回答者を集めるのもコスト的、労力的に大変じゃ。そこでアンケート実施時には、回答者の人数によって変わってくる誤差率を考慮する必要がある。誤差率というのは、文字通りアンケート結果にどの程度の誤差があるかをあらわすもので、精度とは表裏一体の関係にあるものじゃ。
 (精度と誤差率、メモメモ・・・・ )
(精度と誤差率、メモメモ・・・・ ) 例えばさっきのパッケージアンケートを200人に聞く場合、最大で7%程度回答に誤差がでるんじゃ。
例えばさっきのパッケージアンケートを200人に聞く場合、最大で7%程度回答に誤差がでるんじゃ。 アンナさんもそのようなことを言ってました。パパっと計算して、細かいことは聞いても教えてくれませんでしたが・・・。
アンナさんもそのようなことを言ってました。パパっと計算して、細かいことは聞いても教えてくれませんでしたが・・・。 ホッホッホ、あの子は天才肌じゃからのう。ちゃんと計算式があるんじゃよ。
ホッホッホ、あの子は天才肌じゃからのう。ちゃんと計算式があるんじゃよ。
その前にちょっとややこしい話じゃが、同じ質問で、同じ回答人数じゃとしても、その質問の選択肢に回答した割合で誤差率は違うてくることを頭に入れとってくれ。200名回答者がAとBのどちらかを選択する場合、「Aを100名、Bを100名(この場合50%と50%)」のケースと「Aを180名、Bを20名(この場合90%と10%)」のケースでは誤差率が違うということじゃ。
<計算式>
誤差率=
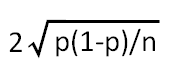
※n=回答者数(サンプル数)
※p=選択肢の回答割合
 これで計算すれば、誤差率が分かるのですね。
これで計算すれば、誤差率が分かるのですね。 まあ毎度計算するのも大変じゃから、誤差率表という便利なものを準備しておくとええわい。サーベイQ、映しとくれ。
まあ毎度計算するのも大変じゃから、誤差率表という便利なものを準備しておくとええわい。サーベイQ、映しとくれ。
 かしこまりました。
かしこまりました。
ピピピ・・・・。
<アンケート回答数の誤差率表>
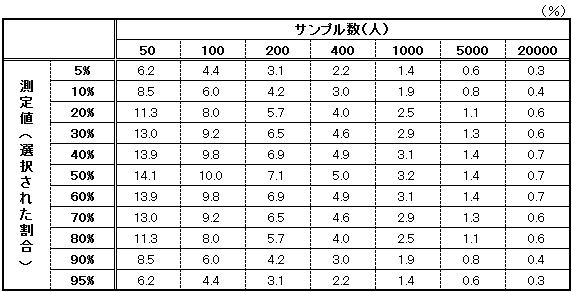
 表頭(上部)が回答者数で、表側(左側)が回答の割合じゃ。それぞれ交差するマスに、誤差率が最大でどの程度出るか書いておる。
表頭(上部)が回答者数で、表側(左側)が回答の割合じゃ。それぞれ交差するマスに、誤差率が最大でどの程度出るか書いておる。 これは便利ですね。ええと・・・、200名で50%の場合は最大誤差率は7.1%。ということは、回答の割合は42.9~57.1%の範囲になるということですね。90%の場合は4.2%。85.8~94.2%の範囲になるということか。
これは便利ですね。ええと・・・、200名で50%の場合は最大誤差率は7.1%。ということは、回答の割合は42.9~57.1%の範囲になるということですね。90%の場合は4.2%。85.8~94.2%の範囲になるということか。
ん・・・?どの回答者数でも共通ですが、回答の割合が50%の時に最も高い誤差率ですね。
 そうじゃの、回答の割合が少ない場合や多い場合は誤差率が低くなるからサンプル数が少なくても大丈夫ということじゃ。200名中デザインAを選んだ回答者が80%、Bを選んだ回答者が20%じゃった場合、誤差率を考慮しても「デザインAは74.3~85.7%」「デザインBは14.3~25.7%」じゃから、十分差があるということが言えるの。
そうじゃの、回答の割合が少ない場合や多い場合は誤差率が低くなるからサンプル数が少なくても大丈夫ということじゃ。200名中デザインAを選んだ回答者が80%、Bを選んだ回答者が20%じゃった場合、誤差率を考慮しても「デザインAは74.3~85.7%」「デザインBは14.3~25.7%」じゃから、十分差があるということが言えるの。
 ということは、誤差率表を見てどの程度の精度が要求されるかによって回答者の人数を決めればいいということですね。
ということは、誤差率表を見てどの程度の精度が要求されるかによって回答者の人数を決めればいいということですね。 その通り。分かってきたようじゃな。ケイト君がわかってきたところで、さっきの誤差率計算と誤差率表を使う際のちょっとした注意点を補足しておこうかの。
その通り。分かってきたようじゃな。ケイト君がわかってきたところで、さっきの誤差率計算と誤差率表を使う際のちょっとした注意点を補足しておこうかの。
実は厳密に言うと、95%の確率で当てはまることを基準にした計算式なんじゃ。つまり20回アンケートをすると、1回ぐらい誤差率を超えてしまうことがあるのじゃよ。
「95%の信頼度」というような言うのじゃが、今はややこしいから説明は別の機会にするわいの。
それともう一つ補足じゃが、今日説明した誤差を推定する方法は「区間推定」というものじゃが、別の精度を調べる方法として「検定」という方法もある。この検定は少し統計の専門的な話になるので、ケイト君がアンケートに慣れてきたら説明しようかの。
今の段階では、誤差率表の見方を覚えておけば大丈夫じゃよ。
 はい、ありがとうございます。(メモメモ・・・アンケートの精度、誤差率・・・・)
はい、ありがとうございます。(メモメモ・・・アンケートの精度、誤差率・・・・)
・・・・・・。
博士、気になったのですが、地域や性別・年齢など属性別で分析することを考慮すると、属性毎に回答者数を集めなくてはいけないということですか?
 それはケースバイケースじゃな。属性別の分析を重視するのであれば誤差が少なくなるように必要に応じたサンプル数を確保しなくてはならんが、属性別分析を参考程度という位置づけであれば対象の属性に30サンプル確保するぐらいでいいんじゃよ。性・年齢別や満足度別など分析を深堀していくと沢山の軸(分け方)がでてくるから、きりがなくなってしまうしの。属性別のサンプル数に関連するんじゃが、アンケートの精度はサンプル数による誤差率ともう一つ重要な要素がある。母集団と標本(サンプル)の関係じゃ。
それはケースバイケースじゃな。属性別の分析を重視するのであれば誤差が少なくなるように必要に応じたサンプル数を確保しなくてはならんが、属性別分析を参考程度という位置づけであれば対象の属性に30サンプル確保するぐらいでいいんじゃよ。性・年齢別や満足度別など分析を深堀していくと沢山の軸(分け方)がでてくるから、きりがなくなってしまうしの。属性別のサンプル数に関連するんじゃが、アンケートの精度はサンプル数による誤差率ともう一つ重要な要素がある。母集団と標本(サンプル)の関係じゃ。
 そういえば、アンナさんに教えてもらいました。
そういえば、アンナさんに教えてもらいました。 おっと、もうこんな時間か。説明を続けたいところじゃが、次の予定がはいっていての。すまんが、そろそろリサが帰ってくるから続きを聞いとくれ。
おっと、もうこんな時間か。説明を続けたいところじゃが、次の予定がはいっていての。すまんが、そろそろリサが帰ってくるから続きを聞いとくれ。
 分かりました。 ありがとうございます。(今のうちに、教えてもらったことをまとめておこう・・・・)
分かりました。 ありがとうございます。(今のうちに、教えてもらったことをまとめておこう・・・・)
(カキカキ・・・・)
 ケイトさん、コーヒーが入りましたよ。
ケイトさん、コーヒーが入りましたよ。 サンキュー、サーベイQ。
サンキュー、サーベイQ。
ゴクリ・・・・。
・・・・・・・
うぇ・・・・・。
・・・・相当甘くない?
 ・・・・・。実は砂糖をこぼしてしまいまして、通常の量より多くなってしまったのでございます。
・・・・・。実は砂糖をこぼしてしまいまして、通常の量より多くなってしまったのでございます。
「95%の信頼度」なので、20回に1回の誤差率の範疇外ということですね・・・、ハイ・・・・。
 ということですねって、ただ失敗しただけじゃん・・・・。相変わらず、どこかヌケているロボだなぁ・・・・。
ということですねって、ただ失敗しただけじゃん・・・・。相変わらず、どこかヌケているロボだなぁ・・・・。
 簡単な調査なら、200人ぐらいで間に合うことが多いのう。場合によっては、100人でも十分な場合もあるわい。少し細かい分析をするなら500人ぐらいかのう。
簡単な調査なら、200人ぐらいで間に合うことが多いのう。場合によっては、100人でも十分な場合もあるわい。少し細かい分析をするなら500人ぐらいかのう。
 ええっ!そんなに少なくていいのですか?1000人ぐらい必要なんじゃないですか?
ええっ!そんなに少なくていいのですか?1000人ぐらい必要なんじゃないですか? もちろん1000人ぐらい必要なケースもあるが、必要な回答人数はどれぐらいの精度を求めるかによるんじゃよ。
もちろん1000人ぐらい必要なケースもあるが、必要な回答人数はどれぐらいの精度を求めるかによるんじゃよ。 精度って、アンケート結果がどれだけ正しいかということですよね。
精度って、アンケート結果がどれだけ正しいかということですよね。 簡単にいうとそうじゃの。例えば商品パッケージを決めるためデザイン候補AとBのアンケートを実施する場合、回答者は5人でいいと思うかい?
簡単にいうとそうじゃの。例えば商品パッケージを決めるためデザイン候補AとBのアンケートを実施する場合、回答者は5人でいいと思うかい?
 それは、少ないような気がします。
それは、少ないような気がします。 じゃあ、100万人の回答者は必要かね?
じゃあ、100万人の回答者は必要かね? 確かに精度は上がりそうですが、それはそれで多すぎて大変そうな気がします。
確かに精度は上がりそうですが、それはそれで多すぎて大変そうな気がします。 そうじゃの。アンケートの回答者、つまりサンプル数は基本的に多ければ多いほど精度は高くなる。だからといって、上限なく回答者を集めるのもコスト的、労力的に大変じゃ。そこでアンケート実施時には、回答者の人数によって変わってくる誤差率を考慮する必要がある。誤差率というのは、文字通りアンケート結果にどの程度の誤差があるかをあらわすもので、精度とは表裏一体の関係にあるものじゃ。
そうじゃの。アンケートの回答者、つまりサンプル数は基本的に多ければ多いほど精度は高くなる。だからといって、上限なく回答者を集めるのもコスト的、労力的に大変じゃ。そこでアンケート実施時には、回答者の人数によって変わってくる誤差率を考慮する必要がある。誤差率というのは、文字通りアンケート結果にどの程度の誤差があるかをあらわすもので、精度とは表裏一体の関係にあるものじゃ。
 (精度と誤差率、メモメモ・・・・ )
(精度と誤差率、メモメモ・・・・ ) 例えばさっきのパッケージアンケートを200人に聞く場合、最大で7%程度回答に誤差がでるんじゃ。
例えばさっきのパッケージアンケートを200人に聞く場合、最大で7%程度回答に誤差がでるんじゃ。 アンナさんもそのようなことを言ってました。パパっと計算して、細かいことは聞いても教えてくれませんでしたが・・・。
アンナさんもそのようなことを言ってました。パパっと計算して、細かいことは聞いても教えてくれませんでしたが・・・。 ホッホッホ、あの子は天才肌じゃからのう。ちゃんと計算式があるんじゃよ。
ホッホッホ、あの子は天才肌じゃからのう。ちゃんと計算式があるんじゃよ。
その前にちょっとややこしい話じゃが、同じ質問で、同じ回答人数じゃとしても、その質問の選択肢に回答した割合で誤差率は違うてくることを頭に入れとってくれ。200名回答者がAとBのどちらかを選択する場合、「Aを100名、Bを100名(この場合50%と50%)」のケースと「Aを180名、Bを20名(この場合90%と10%)」のケースでは誤差率が違うということじゃ。
<計算式>
誤差率=
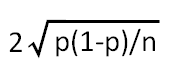
※n=回答者数(サンプル数)
※p=選択肢の回答割合
 これで計算すれば、誤差率が分かるのですね。
これで計算すれば、誤差率が分かるのですね。 まあ毎度計算するのも大変じゃから、誤差率表という便利なものを準備しておくとええわい。サーベイQ、映しとくれ。
まあ毎度計算するのも大変じゃから、誤差率表という便利なものを準備しておくとええわい。サーベイQ、映しとくれ。
 かしこまりました。
かしこまりました。
ピピピ・・・・。
<アンケート回答数の誤差率表>

 表頭(上部)が回答者数で、表側(左側)が回答の割合じゃ。それぞれ交差するマスに、誤差率が最大でどの程度出るか書いておる。
表頭(上部)が回答者数で、表側(左側)が回答の割合じゃ。それぞれ交差するマスに、誤差率が最大でどの程度出るか書いておる。 これは便利ですね。ええと・・・、200名で50%の場合は最大誤差率は7.1%。ということは、回答の割合は42.9~57.1%の範囲になるということですね。90%の場合は4.2%。85.8~94.2%の範囲になるということか。
これは便利ですね。ええと・・・、200名で50%の場合は最大誤差率は7.1%。ということは、回答の割合は42.9~57.1%の範囲になるということですね。90%の場合は4.2%。85.8~94.2%の範囲になるということか。
ん・・・?どの回答者数でも共通ですが、回答の割合が50%の時に最も高い誤差率ですね。
 そうじゃの、回答の割合が少ない場合や多い場合は誤差率が低くなるからサンプル数が少なくても大丈夫ということじゃ。200名中デザインAを選んだ回答者が80%、Bを選んだ回答者が20%じゃった場合、誤差率を考慮しても「デザインAは74.3~85.7%」「デザインBは14.3~25.7%」じゃから、十分差があるということが言えるの。
そうじゃの、回答の割合が少ない場合や多い場合は誤差率が低くなるからサンプル数が少なくても大丈夫ということじゃ。200名中デザインAを選んだ回答者が80%、Bを選んだ回答者が20%じゃった場合、誤差率を考慮しても「デザインAは74.3~85.7%」「デザインBは14.3~25.7%」じゃから、十分差があるということが言えるの。
 ということは、誤差率表を見てどの程度の精度が要求されるかによって回答者の人数を決めればいいということですね。
ということは、誤差率表を見てどの程度の精度が要求されるかによって回答者の人数を決めればいいということですね。 その通り。分かってきたようじゃな。ケイト君がわかってきたところで、さっきの誤差率計算と誤差率表を使う際のちょっとした注意点を補足しておこうかの。
その通り。分かってきたようじゃな。ケイト君がわかってきたところで、さっきの誤差率計算と誤差率表を使う際のちょっとした注意点を補足しておこうかの。
実は厳密に言うと、95%の確率で当てはまることを基準にした計算式なんじゃ。つまり20回アンケートをすると、1回ぐらい誤差率を超えてしまうことがあるのじゃよ。
「95%の信頼度」というような言うのじゃが、今はややこしいから説明は別の機会にするわいの。
それともう一つ補足じゃが、今日説明した誤差を推定する方法は「区間推定」というものじゃが、別の精度を調べる方法として「検定」という方法もある。この検定は少し統計の専門的な話になるので、ケイト君がアンケートに慣れてきたら説明しようかの。
今の段階では、誤差率表の見方を覚えておけば大丈夫じゃよ。
 はい、ありがとうございます。(メモメモ・・・アンケートの精度、誤差率・・・・)
はい、ありがとうございます。(メモメモ・・・アンケートの精度、誤差率・・・・)
・・・・・・。
博士、気になったのですが、地域や性別・年齢など属性別で分析することを考慮すると、属性毎に回答者数を集めなくてはいけないということですか?
 それはケースバイケースじゃな。属性別の分析を重視するのであれば誤差が少なくなるように必要に応じたサンプル数を確保しなくてはならんが、属性別分析を参考程度という位置づけであれば対象の属性に30サンプル確保するぐらいでいいんじゃよ。性・年齢別や満足度別など分析を深堀していくと沢山の軸(分け方)がでてくるから、きりがなくなってしまうしの。属性別のサンプル数に関連するんじゃが、アンケートの精度はサンプル数による誤差率ともう一つ重要な要素がある。母集団と標本(サンプル)の関係じゃ。
それはケースバイケースじゃな。属性別の分析を重視するのであれば誤差が少なくなるように必要に応じたサンプル数を確保しなくてはならんが、属性別分析を参考程度という位置づけであれば対象の属性に30サンプル確保するぐらいでいいんじゃよ。性・年齢別や満足度別など分析を深堀していくと沢山の軸(分け方)がでてくるから、きりがなくなってしまうしの。属性別のサンプル数に関連するんじゃが、アンケートの精度はサンプル数による誤差率ともう一つ重要な要素がある。母集団と標本(サンプル)の関係じゃ。
 そういえば、アンナさんに教えてもらいました。
そういえば、アンナさんに教えてもらいました。 おっと、もうこんな時間か。説明を続けたいところじゃが、次の予定がはいっていての。すまんが、そろそろリサが帰ってくるから続きを聞いとくれ。
おっと、もうこんな時間か。説明を続けたいところじゃが、次の予定がはいっていての。すまんが、そろそろリサが帰ってくるから続きを聞いとくれ。
 分かりました。 ありがとうございます。(今のうちに、教えてもらったことをまとめておこう・・・・)
分かりました。 ありがとうございます。(今のうちに、教えてもらったことをまとめておこう・・・・)
(カキカキ・・・・)
 ケイトさん、コーヒーが入りましたよ。
ケイトさん、コーヒーが入りましたよ。 サンキュー、サーベイQ。
サンキュー、サーベイQ。
ゴクリ・・・・。
・・・・・・・
うぇ・・・・・。
・・・・相当甘くない?
 ・・・・・。実は砂糖をこぼしてしまいまして、通常の量より多くなってしまったのでございます。
・・・・・。実は砂糖をこぼしてしまいまして、通常の量より多くなってしまったのでございます。
「95%の信頼度」なので、20回に1回の誤差率の範疇外ということですね・・・、ハイ・・・・。
 ということですねって、ただ失敗しただけじゃん・・・・。相変わらず、どこかヌケているロボだなぁ・・・・。
ということですねって、ただ失敗しただけじゃん・・・・。相変わらず、どこかヌケているロボだなぁ・・・・。
